Distanza di un punto da una retta

Come si calcola la distanza di un punto da una retta? Innanzitutto dato un punto P e una retta r la distanza \(d(P,r)\) è la lunghezza del segmento PH sulla perpendicolare alla retta che passa per il punto P.

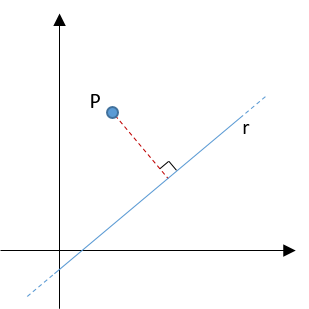
Per calcolare tale distanza procediamo come segue:

Se abbiamo una retta r in forma esplicita \(y=mx+q\) portiamola in forma implicita \(ax+bx+c=0\) semplicemente portando tutti i termini a sinistra dell’uguale. Se è già in forma esplicita non dobbiamo fare questo passaggio.

A questo punto la distanza del punto \(P(x_0;y_0)\) dalla retta \(r:ax+by+c=0\) è data dalla formula