Disegnare una retta

Vediamo un paio di modi utili per tracciare il grafico di una retta data la sua equazione. Il primo modo sfrutta il significato del coefficiente angolare m e dell’ordinata all’origine q. Il secondo modo consiste semplicemente nel trovare due punti della retta e tracciare dunque l’unica retta che passa per essi.

1) Sfruttando il significato di m e q

Abbiamo visto che la q indica il punto in cui la retta taglia l’asse y: sappiamo dunque che la retta passerà per il punto $Q(0;q)$. Ora sfruttiamo la definizione di m: è il rapporto tra quanto aumenta la y diviso quanto aumenta la x nel passare da un punto all’altro sulla retta. Se aumentiamo la x di 1 allora la m sarà quanto aumenta la y diviso 1 cioè esattamente quanto aumenta la y!

Poniamoci quindi nel punto $Q(0;q)$ che sappiamo appartenere alla retta, spostiamoci a destra di 1 (cioè aumentiamo la x di 1) e verso l’alto di m (cioè la y aumenta di m). Se la m è negativa dovremo naturalmente verso il basso. Siamo arrivati così ad un altro punto della retta: basterà collegarlo con quello sull’asse y per tracciare la retta.

Esempio:

Disegniamo la retta

$$y=2x+1$$

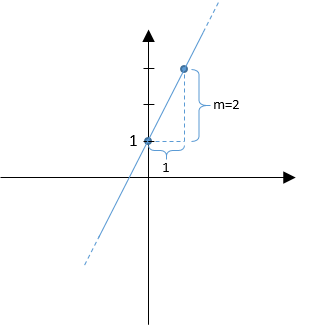
Essa passa taglia l’asse y nel punto di ordinata 1 (perché $q=1$)

Il punto di intersezione con l'asse y è in Q(0;1)

Da questo punto spostiamoci a destra di uno e verso l’alto di 2 (perché $m=2$). Tracciamo infine la retta dal punto di prima al punto dove siamo arrivati adesso

Il coefficiente angolare dà indicazioni sulla pendenza della retta

2) Trovando dei punti sulla retta

Il secondo modo consiste nel trovare dei punti appartenenti alla retta e tracciare quindi quest’ultima allineandovi il righello.

Naturalmente basta trovare due punti (per due punti passa una e una sola retta) ma ne troveremo tre per avere un piccolo controllo (se i punti non sono tutti e tre allineati abbiamo sbagliato qualcosa) e perché così è più facile allineare bene il righello ed evitare di tracciare una retta storta.

Esempio:

Disegniamo la retta

$$y=2x+1$$

Se vogliamo ad esempio trovare il punto P che sta sulla retta ed ha ascissa x=1 basta inserire tale valore di x nell’equazione della retta per trovare la sua y, cioè se $P(x_P;y_P)$ ha $x_P=1$ quanto deve essere $y_P$ se il punto deve stare sulla retta? Sostituisco e ottengo $y_P=2\cdot 1 \ +1$ quindi $y_P=3$ e il punto $P(1,3)$ è il primo punto cercato. Ripetiamo l’operazione per altri due punti ad esempio quelli di ascissa 0 e -1 e riportiamo i valori in una tabella per comodità e disegniamoli sul grafico:

Disegno i tre punti sul grafico

Infinine è sufficiente tracciare la retta che passa per i tre punti

Traccio la retta che vi passa