Equazioni con valore assoluto
Vediamo ora come si risolvono le equazioni che contengono almeno un'espressione in valore assoluto come ad esempio l'equazione $$ \lvert 2x+6\rvert = x-2$$ o l'equazione $$\lvert x+2\rvert = \lvert x+7\rvert. $$ Per risolvere questo tipo di equazioni è necessario dividere in vari casi la risoluzione a seconda dei segni degli argomenti dei valori assoluti. Infine bisogna verificare che la soluzione sia accettabile (cioè rientri nel caso che si sta studiando). Iniziamo con le equazioni in cui compare una sola espressione in valore assoluto.Equazioni con un solo valore assoluto
Un'equazione di questo tipo è equivalente a due equazioni in cui analizziamo separatamente i due casi che si ottengono a seconda che l'argomento del valore assoluto sia positivo o negativo.
Risolviamo ad esempio l'equazione
Nel caso ci siano più valori assoluti uno dentro l'altro si inizia da quello più interno dividendo i due casi, poi a sua volta per ognuno dei due casi si studia il valore assoluto più esterno.
$$ \lvert x-2\rvert=2x+1$$
L'argomento del valore assoluto è \(x-2\), è positivo per \(x \ge 2\) e negativo per \(x \lt 2 \).
- Primo caso: \(x \ge 2\)
In questo caso l'argomento del valore assoluto è positivo e non occorre cambiargli segno. L'equazione diventa $$x - 2 = 2x+1$$ $$x = -3$$ La soluzione \(x=-3\) non è però accettabile perché non è maggiore o uguale a 2. - Secondo caso: \(x\lt 2\)
L'argomento del valore assoluto è negativo quindi per renderlo positivo bisogna mettere un meno davanti, ovvero cambiare tutti i segni: \(-(x-2) \rightarrow -x+2\) L'equazione diventa $$-x+2 = 2x+1$$ $$-3x=-1$$ $$x=\frac{1}{3}$$ In questo caso la soluzione \( x=\frac{1}{3} \) è accettabile poiché è minore di 2, cioè rientra nel caso che stiamo studiando.
Risolviamo ad esempio l'equazione:
$$\lvert \lvert x+5\rvert -x \rvert = -x+2 $$
Studiamo il segno del valore assoluto più interno e dividiamo i due casi. L'argomento del valore assoluto più interno è \(x+5\), positivo per \(x \ge -5\) e negativo per \(x \lt -5 \).
- Primo caso: \(x \ge -5\)
In questo caso l'argomento del valore assoluto è positivo e non occorre cambiargli segno. Si ottiene quindi: $$ \require{cancel}$$ $$\lvert \cancel{x}+5-\cancel{x} \rvert = -x+2$$ $$5 = -x +2$$ $$x=-3$$ E la soluzione \(x=-3\) è accettabile in quanto maggiore o uguale a -5. - Secondo caso: \(x \lt -5\)
In questo caso dobbiamo invertire il segno dell'argomento del valore assoluto interno moltiplicando tutto per -1. Si ottiene: $$\lvert -(x+5)-x \rvert = -x+2$$ $$\lvert -x-5-x \rvert = -x+2$$ $$\lvert -2x-5\rvert = -x+2$$ Ci siamo così ricondotti ad un'equazione con un solo valore assoluto. La risolviamo come abbiamo visto prima ricordandoci però della condizione che descrive il caso in cui ci troviamo: \(x \lt -5\). L'argomento del valore assoluto è \(-2x-5\), positivo per \(x \le -\frac{5}{2}\) e negativo sull'intervallo complementare \(x > -\frac{5}{2} \).- Primo sottocaso: \(x \le -\frac{5}{2}\)
L'argomento del valore assoluto è già positivo in questo caso. SI ottiene: $$-2x-5 = -x+2$$ $$-x = 7$$ $$x=-7$$ La soluzione $$x=-7$$ è sia minore o uguale a \(-\frac{5}{2}\), cioè rientra nel sottocaso che stiamo studiando sia minore di -5, cioè rientra nel caso generale in cui avevamo diviso lo studio in precedenza. È dunque una soluzione accettabile. - Secondo sottocaso: \(x > -\frac{5}{2}\)
Invertiamo il segno dell'argomento del valore assoluto moltiplicando tutto per -1. Si ottiene: $$2x+5=-x+2$$ $$3x=-3$$ $$x=-1$$ La soluzione \(x=-1\) rientra in questo sottocaso poiché è maggiore di \(-\frac{5}{2}\) ma non rientra nel caso generale in cui eravamo, infatti non è minore di -5. Dunque non è una soluzione accettabile.
- Primo sottocaso: \(x \le -\frac{5}{2}\)
Equazioni con più valori assoluti
Se vi sono più valori assoluti bisogna, come prima, capire il segno dei vari argomenti al variare della \(x\), riassumere il tutto in una tabella e studiare infine i casi trovati, che adesso possono essere più di due. Ogni volta, ricordiamo, bisogna controllare che la soluzione sia ammissibile cioè rientri nel caso che si sta studiando. Vediamo un esempio.
Risolviamo l'equazione
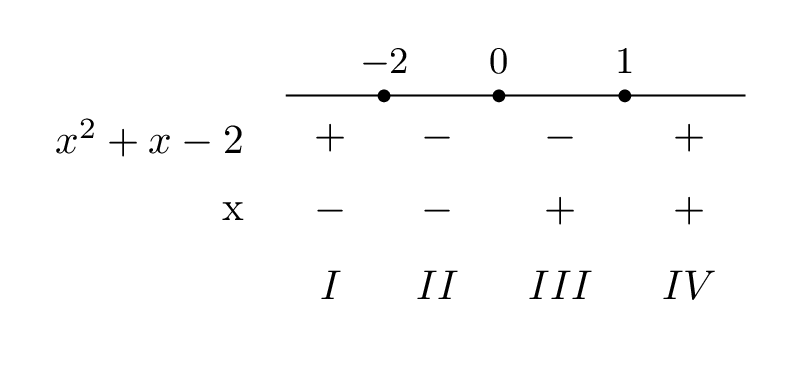 Abbiamo quindi quattro casi diversi da studiare, che corrispondono ai sottoinsiemi in cui abbiamo diviso la retta reale.
Abbiamo quindi quattro casi diversi da studiare, che corrispondono ai sottoinsiemi in cui abbiamo diviso la retta reale.
$$\lvert x^2+x-2 \rvert = \lvert x \rvert +2$$
L'argomento del primo valore assoluto è \(x^2+2-2\), risolviamo la disequazione di secondo grado \(x^2+2-2 \ge 0\) per capire quando è positivo. Otteniamo che è positivo per \(x \le -2\) o \(x \ge 1\).
L'argomento dell'altro valore assoluto è semplicemente \(x\), ovviamente positivo se \(x \ge 0\) e negativo altrimenti. Riassumiamo tutto in una tabella dei segni
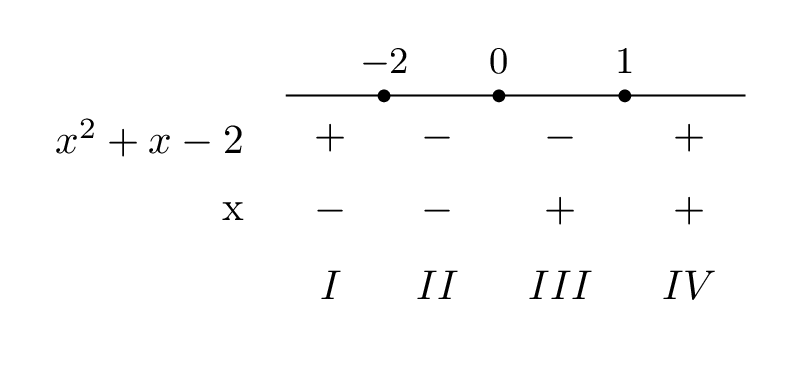 Abbiamo quindi quattro casi diversi da studiare, che corrispondono ai sottoinsiemi in cui abbiamo diviso la retta reale.
Abbiamo quindi quattro casi diversi da studiare, che corrispondono ai sottoinsiemi in cui abbiamo diviso la retta reale.
- Caso I: \(x \lt -2\)
(Nota: qui escludiamo il valore \(-2\), ma lo consideriamo nel caso II. In generale non importa dove mettiamo i \(\lt \) o \(\le\), l'importante è che in almeno uno dei casi questi valori vengano considerati, in modo da ottenere effettivamente una partizione di \(\mathbb{R}\))
In questo caso l'argomento del primo valore assoluto è già positivo e non occorre cambiargli segno. Bisogna invece cambiare segno all'argomento del secondo valore assoluto, cioè \(x\) (\(2\) è fuori dal valore assoluto, pertanto non viene modificato). Otteniamo: $$x^2+x-2=-x +2$$ $$x^2+2x-4=0$$ Risolvendo l'equazione di secondo grado si ottiene \(x_1=-1+\sqrt{5}\) e \(x_2=-1+\sqrt{5}\). Di queste solo \(x_2=-1-\sqrt{5}\) soddisfa la condizione \(x \lt 2\) ed è pertanto accettabile. - Caso II: \(-2 \le x \lt 0\)
Dobbiamo cambiare il segno ad entrambi gli argomenti. Otteniamo: $$-x^2-x+2=-x+2$$ $$-x^2=0$$ La cui soluzione è \(X=0\). Essa però non soddisfa la condizione \(-2 \le x \lt 0\) pertanto non è accettabile. - Caso III: \(0 \le x \lt 1\)
In questo caso dobbiamo cambiare il segno del primo argomento. Otteniamo: $$-x^2-x+2=x+2$$ $$-x^2-2x=0$$ $$x(x+2)=0$$ Che ha come soluzioni \(x=0\) e \(x=-2\). Di queste solo \(x=0\) soddisfa la condizione \(0 \le x \lt 1\), dunque è l'unica accettabile. - Caso IV: \(x \ge 1\)
In questo caso essendo gli argomenti già positivi non dobbiamo cambiare il segno di nessun termine: $$x^2+x-2=x+2$$ $$x^2=4$$ Risolvendo l'equazione di secondo grado si ottiene \(x_1=-2\) e \(x_2=2\). Di queste solo \(x_2=2\) soddisfa la condizione \(x > 1\) quindi è l'unica accettabile.