Disequazioni fratte
Una disequazione si dice fratta se l'incognita \( x\) compare al denominatore.Ad esempio le disequazioni $$ \frac{x^2+3x-4}{x+5} \ge 0; \qquad \frac{2x-5}{x}+1 \lt -1$$ sono disequazioni fratte.
La prima cosa da fare è riportarci ad un'equazione del tipo $$\frac{A(x)}{B(x)} \gt 0$$ (o uno qualsiasi degli altri segni di disuguaglianza) portando tutti i termini a sinistra e facendo il minimo comune denominatore.
Attenzione
In questo tipo di disequazioni non possiamo semplicemente moltiplicare per il denominatore in modo da "toglierlo",
infatti non conosciamo il suo segno (o meglio, essendondoci la \(x \), il segno del denominatore varia) e dunque non sappiamo
se stiamo moltiplicando entrambi i lati della disequazione per un numero positivo oppure per un numero negativo e dobbiamo cambiare
il verso della disuguaglianza.
Nota
Poichè ci sono dei denominatori dobbiamo prima di tutto imporre delle condizioni di esistenza delle frazioni, ovvero richiedere che i denominatori siano diversi da 0.
Alla fine dovremo confrontare la soluzione ottenuta con le condizioni di esistenza.
Esempi di disequazioni fratte
1) Risolviamo la disequazione fratta
$$ \frac{x^2+3x-4}{x+5} \ge 0$$
Poichè c'è un denominatore e la divisione per 0 non è definita iniziamo con il richiedere le condizioni di esistenza:C.E.: \(x+5 \neq 0 \rightarrow x \neq -5\)
A questo punto siccome abbiamo già una disequazione nella forma \(A(x)/B(x) \ge 0 \) studiamo separatamente il segno del numeratore e il segno del denominatore.
N) Iniziamo dal numeratore:
\(x^2+3x-4 \ge 0 \) è una disequazione di secondo grado (vai a vedere la pagina relativa se non ricordi come si svolgono) che ha come soluzione \(x \le -4 \lor x \ge 1\)
D) Mentre per il denominatore (cerchiamo solo quando è strettamente positivo, dato che se è uguale a 0 la frazione non esiste):
\(x+5 \gt 0 \rightarrow x \gt -5\) Riportiamo i segni trovati in uno schema dei segni:
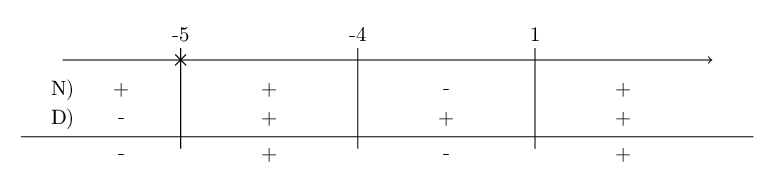 La nostra disequazione di partenza chiedeva di trovare quando la frazione è maggiore o uguale a zero. Quindi ci interessano gli intevalli dove abbiamo segnato un "+", estremi inclusi, ma dobbiamo però escludere i valori che avevamo escluso inizialmente con le condizioni di esistenza (ovvero il valore -5 in questo caso).
In conclusione la soluzione della disequazione è
$$-5 \lt x \le -4 \quad \lor \quad x \ge 1$$
La nostra disequazione di partenza chiedeva di trovare quando la frazione è maggiore o uguale a zero. Quindi ci interessano gli intevalli dove abbiamo segnato un "+", estremi inclusi, ma dobbiamo però escludere i valori che avevamo escluso inizialmente con le condizioni di esistenza (ovvero il valore -5 in questo caso).
In conclusione la soluzione della disequazione è
$$-5 \lt x \le -4 \quad \lor \quad x \ge 1$$
2) Risolviamo la disequazione fratta
$$ \frac{2x-5}{x}+1 \lt -1$$
Per prima cosa imponiamo le condizioni di esistenza (denominatori diversi da 0).C.E.: \(x \neq 0\).
A questo punto facciamo il minimo comune denominatore per riportarci alla forma \(A(x)/B(x) \lt 0 \)
$$ \frac{2x-5 }{x} +2 \lt 0 \quad \rightarrow \quad \frac{2x-5 +2x }{x}\lt 0 \quad \rightarrow \quad \frac{4x-5}{x}\lt 0 $$
Studiamo separatamente i segni di numeratore e denominatore:
N) \( 4x-5 \gt 0 \rightarrow x \gt \frac{5}{4}\)
D) \(x \gt 0 \)
Riportiamo i risultati in uno schema dei segni
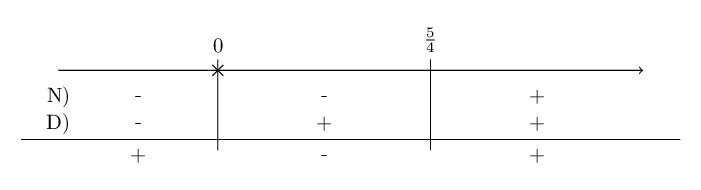 A noi interessa quando la frazione è strettamente minore di 0. Prendiamo quindi gli intervalli in cui abbiamo segnato un "-", estremi esclusi. La condizione di esistenza era \(x \neq 0\) e tale valore è gia escluso dall'insieme delle soluzione.
La soluzione della disequazione è pertanto
$$0 \lt x \lt \frac{5}{4} $$
A noi interessa quando la frazione è strettamente minore di 0. Prendiamo quindi gli intervalli in cui abbiamo segnato un "-", estremi esclusi. La condizione di esistenza era \(x \neq 0\) e tale valore è gia escluso dall'insieme delle soluzione.
La soluzione della disequazione è pertanto
$$0 \lt x \lt \frac{5}{4} $$