Funzioni inverse

Abbiamo visto che una funzione è una corrispondenza che ad ogni elemento del dominio associa uno e un solo elemento del codominio.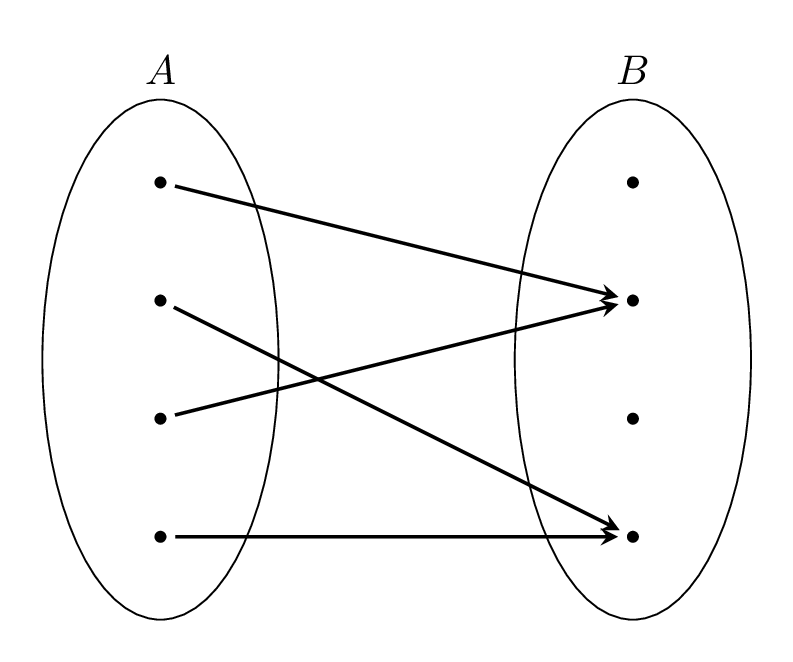 Se provassimo a vedere la funzione all'inverso, ovvero scambiando dominio e codominio ed invertendo tutte le frecce non è detto che otterremmo ancora una funzione, infatti le due richieste della definizione potrebbero non essere soddisfatte. Potrebbero esserci elementi del nuovo dominio a cui non viene associato niente oppure da un elemento potrebbero partire due frecce.

Quando una funzione \(f\) è iniettiva e suriettiva (cioè è biunivoca) questo procedimento va a buon fine ed è quindi possibile definire la funzione inversa di \(f\) che si indica con il simbolo \(f^{-1}\). Una funzione biunivoca è dunque invertibile.

Se \(f(x)=y\) la funzione inversa \(f^{-1}\) associa ad \(y\) la sua controimmagine \(x\), cioè \(f^{-1}(y)=x\).

Se abbiamo l'equazione \(y=f(x)\) della funzione \(f\) e riusciamo a ricavare la \(x\) otteniamo un'equazione \(x=f^{-1}(y)\) che sarà l'equazione della funzione inversa. A questo punto siccome siamo abituati a chiamare \(x\) la variabile indipendente e \(y\) quella dipendente possiamo semplicemente fare la sostituzione che scambia i nomi delle due variabili per ottenere un'espressione del tipo \(y=f^{-1}(x)\).